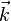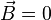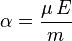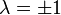Информация о защитах ВКР (2011) — различия между версиями
Материал из Квантовые процессы в астрофизической среде
Okrugin (обсуждение | вклад) |
Okrugin (обсуждение | вклад) |
||
| Строка 53: | Строка 53: | ||
|sciadvisor=Михеев Николай Владимирович, профессор, зав. кафедрой теор. физики, д. ф.‐м. н. | |sciadvisor=Михеев Николай Владимирович, профессор, зав. кафедрой теор. физики, д. ф.‐м. н. | ||
|subj=Дисперсия нейтрино с магнитном моментом в электромагнитном поле | |subj=Дисперсия нейтрино с магнитном моментом в электромагнитном поле | ||
| − | |abstract=:<i>В ходе данной работы получено уравнение Дирака и рассмотрены два случая: 1) при отсутствии электромагнитного поля; 2) с учётом электромагнитного поля. В первом случае были найдены значения энергии нейтрино. Во втором случае были найдены значения энергии нейтрино с учётом его магнитного момента в электромагнитном поле. Было показано, что в электрическом поле, т. е. <math>\vec{B}=0</math>, безразмерной величине <math>\alpha=\frac{\mu\,E}{m}</math>, определяющей значения энергии нейтрино, соответствует две возможные поляризации <math>\lambda=\pm 1</math>, что в свою очередь говорит о том, что нейтрино может находиться в двух состояниях со спином, направленным вдоль или против поля. | + | |abstract=:<i>В ходе данной работы получено уравнение Дирака и рассмотрены два случая: 1) при отсутствии электромагнитного поля; 2) с учётом электромагнитного поля. В первом случае были найдены значения энергии нейтрино. Во втором случае были найдены значения энергии нейтрино с учётом его магнитного момента в электромагнитном поле. Было показано, что в электрическом поле, т. е. <span style="vertical-align:+0.9ex;"><math>\vec{B}=0</math></span>, безразмерной величине <span style="vertical-align:+0.6ex;"><math>\alpha=\frac{\mu\,E}{m}</math></span>, определяющей значения энергии нейтрино, соответствует две возможные поляризации <span style="vertical-align:+0.4ex;"><math>\lambda=\pm 1</math></span>, что в свою очередь говорит о том, что нейтрино может находиться в двух состояниях со спином, направленным вдоль или против поля. |
</i> | </i> | ||
|img=[[Файл:Sledkova_P_A.jpg|180px|border|center|Следкова Полина Андреевна]]}} | |img=[[Файл:Sledkova_P_A.jpg|180px|border|center|Следкова Полина Андреевна]]}} | ||
| Строка 122: | Строка 122: | ||
|sciadvisor=Пархоменко Александр Яковлевич, доцент кафедры теор. физики, к. ф.‐м. н. | |sciadvisor=Пархоменко Александр Яковлевич, доцент кафедры теор. физики, к. ф.‐м. н. | ||
|subj=Константа распада В‐мезона из правил сумм КХД | |subj=Константа распада В‐мезона из правил сумм КХД | ||
| − | |abstract=:<i>. | + | |abstract=:<i>В настоящее время значение константы распада B‐мезона f<sub>B</sub> экспериментально извлекается из относительной вероятности распада B<sup>+</sup> → τ<sup>+</sup> ν<sub>τ</sub>. Полученная оценка превосходит имеющиеся теоретические предсказания. В недавней работе Ву и др. была проанализирована чувствительность константы распада к выбору интерполяционного тока и, в частности, было показано, что при использовании кирального тока значение f<sub>B</sub> заметно увеличивается. Данный анализ проводился методом правил сумм КХД, в рамках которого была выявлена существенная зависимость от величины массы b‐кварка. |
| − | :. | + | :В данной работе на основе дальнейшего обобщения интерполяционного тока B‐мезона посредством параметризации векторной части произвольной константой <math>a</math> построены правила сумм КХД для константы распада f<sub>B</sub>. Метод правил сумм КХД разобран на примере вычисления пертурбативной части соответствующего коррелятора. Получена зависимость константы распада f<sub>B</sub> от параметра <math>a</math>. Проведено сравнение с феноменологическим значением f<sub>B</sub> и показано, что векторная часть должна существенно доминировать в интерполяционном токе, так как численно <math>a</math> ∼ 7. Представляется интересным провести подобный анализ правил сумм при учете непертурбативных эффектов, которые включаются в виде членов, содержащих вакуумные конденсаты кварковых и глюонных полей.</i> |
| − | + | ||
| − | + | ||
|img=[[Файл:Noimage.gif|180px|center|]]}} | |img=[[Файл:Noimage.gif|180px|center|]]}} | ||
| Строка 133: | Строка 131: | ||
|sciadvisor=Кузнецов Владимир Степанович, доцент кафедры теор. физики, к. ф.‐м. н. | |sciadvisor=Кузнецов Владимир Степанович, доцент кафедры теор. физики, к. ф.‐м. н. | ||
|subj=Квазистационарные состояния в квантовой механике | |subj=Квазистационарные состояния в квантовой механике | ||
| − | |abstract=:<i>. | + | |abstract=:<i>В работе проведено рассмотрение туннельного эффекта в квантовой механике. Найден коэффициент прохождения частицы через потенциальную яму и одномерный потенциальный барьер. Изучены квазистационарные состояния в квантовой механике. Вычисление времени жизни частицы в этом состоянии. |
| − | :. | + | :В ходе решения первой задачи было выяснено, что прохождение частицы через потенциальный барьер возможно, если энергия частицы меньше высоты барьера. |
| − | :.</i> | + | :Во второй задаче было получено, что при увеличении энергии коэффициент прохождения стремится к 1. Это значит, что почти все частицы проходят над ямой. Внутри ямы имеет место осциллирующее решение, чем глубже яма, тем больше осцилляции, а вне ямы волновая функция «просачивается» наружу. А с ростом глубины ямы, число уровней энергии и связанных состояний будет увеличиваться, а вероятность обнаружения частицы внутри ямы будет становиться все меньше, а при стремлении в глубины ямы в бесконечность она обратится в ноль. Число уровней всегда конечно и определяется глубиной и шириной потенциальной ямы. |
| + | |||
| + | :В третьей задаче получили, что чем выше уровни энергии над ямой, тем меньше время жизни частицы на этом уровне.</i> | ||
|img=[[Файл:Shilova_N_S.jpg|180px|border|center|Шилова Наталья Сергеевна]]}} | |img=[[Файл:Shilova_N_S.jpg|180px|border|center|Шилова Наталья Сергеевна]]}} | ||
| Строка 158: | Строка 158: | ||
|sciadvisor=Румянцев Дмитрий Александрович, доцент кафедры теор. физики, к. ф.‐м. н. | |sciadvisor=Румянцев Дмитрий Александрович, доцент кафедры теор. физики, к. ф.‐м. н. | ||
|subj=Резонансное рождение электрон‐позитронных пар в магнитосфере магнитара | |subj=Резонансное рождение электрон‐позитронных пар в магнитосфере магнитара | ||
| − | |abstract=:<i>. | + | |abstract=:<i>В работе рассмотрен комптоноподобный процесс рождения электрон‐позитронных пар в случае, когда конечные фермионы находятся на основном уровне Ландау. Вычислена амплитуда этого процесса в случаях, когда виртуальных электрон находится на основном и на первом уровне Ландау, показано, что в последнем случае имеет место резонанс, рассчитана скорость резонансного рождения электрон‐позитронных пар, проведено сравнение результата с предсказаниями магнитарной модели. |
| − | :. | + | :Полученный результат для скорости рождения электрон‐позитронных пар показывает, что рассматриваемый процесс может играть существенную роль в генерации электрон‐позитронной плазмы в магнитосфере магнитара. Имеет смысл в дальнейшем рассмотреть более общий случай, когда конечные фермионы и виртуальный электрон находятся на произвольных уровнях Ландау.</i> |
| − | + | ||
| − | + | ||
|img=[[Файл:Stus'_N_S.jpg|180px|border|center|Стусь Наталья Сергеевна]]}} | |img=[[Файл:Stus'_N_S.jpg|180px|border|center|Стусь Наталья Сергеевна]]}} | ||
Версия 02:09, 13 июля 2011
Курсовые работы, 3‐й курс
| Аминов Дмитрий Владимирович | |
| Научный руководитель — Гвоздев Александр Александрович, доцент кафедры теор. физики, к. ф.‐м. н. | |
| Тема: «Нерелятивистская заряженная частица в постоянном однородном магнитном поле». | |
Аннотация:
|
| Блинова Анна Михайловна | |
| Научный руководитель — Смирнов Александр Дмитриевич, профессор кафедры теор. физики, д. ф.‐м. н. | |
| Тема: «Плоские волны в теории неабелевого калибровочного поля». | |
Аннотация:
|
| Дурандин Михаил Иванович | |
| Научный руководитель — Кузнецов Александр Васильевич, профессор кафедры теор. физики, д. ф.‐м. н. | |
| Тема: «Дзета змееносца и её партнёр — история разрыва». | |
Аннотация:
|
| Епихин Дмитрий Вячеславович | |
| Научный руководитель — Кузнецов Владимир Степанович, доцент кафедры теор. физики, к. ф.‐м. н. | |
| Тема: «Расчёт зонной структуры твердого тела». | |
Аннотация:
|
| Следкова Полина Андреевна | |
| Научный руководитель — Михеев Николай Владимирович, профессор, зав. кафедрой теор. физики, д. ф.‐м. н. | |
| Тема: «Дисперсия нейтрино с магнитном моментом в электромагнитном поле». | |
Аннотация:
|
| Шленев Денис Михайлович | |
| Научный руководитель — Румянцев Дмитрий Александрович, доцент кафедры теор. физики, к. ф.‐м. н. | |
| Тема: «Электродинамика в веществе с учётом разложения по мультипольным моментам». | |
Аннотация:
|
| Яргина Ксения Игоревна | |
| Научный руководитель — Пархоменко Александр Яковлевич, доцент кафедры теор. физики, к. ф.‐м. н. | |
| Тема: «Функция Грина в квантовой механике». | |
Аннотация:
|
Выпускные работы бакалавров
| Беляев Василий Андреевич | |
| Научный руководитель — Гвоздев Александр Александрович, доцент кафедры теор. физики, к. ф.‐м. н. | |
| Тема: «Уравнение состояния вырожденного кваркового газа». | |
Аннотация:
|
| Мазалецкий Леонид Алексеевич | |
| Научный руководитель — Смирнов Александр Дмитриевич, профессор кафедры теор. физики, д. ф.‐м. н. | |
| Тема: «Рождение пар частиц в e+ e-‐столкновениях». | |
Аннотация:
|
| Мосичкин Анатолий Фёдорович | |
| Научный руководитель — Кузнецов Владимир Степанович, доцент кафедры теор. физики, к. ф.‐м. н. | |
| Тема: «Процессы самоорганизации в полупроводниках в сильном электрическом поле». | |
Аннотация:
|
| Радченко Мария Сергеевна | |
| Научный руководитель — Кузнецов Александр Васильевич, профессор кафедры теор. физики, д. ф.‐м. н. | |
| Тема: «Квантовые алгоритмы для трудно решаемых задач». | |
Аннотация:
|
| Русов Алексей Валерьевич | |
| Научный руководитель — Пархоменко Александр Яковлевич, доцент кафедры теор. физики, к. ф.‐м. н. | |
| Тема: «Константа распада В‐мезона из правил сумм КХД». | |
Аннотация:
|
| Шилова Наталья Сергеевна | |
| Научный руководитель — Кузнецов Владимир Степанович, доцент кафедры теор. физики, к. ф.‐м. н. | |
| Тема: «Квазистационарные состояния в квантовой механике». | |
Аннотация:
|
Магистерские диссертации
| Капитонова Елена Сергеевна | |
| Научный руководитель — Кузнецов Владимир Степанович, доцент кафедры теор. физики, к. ф.‐м. н. | |
| Тема: «Токовые неустойчивости в кремнии в области сильных электрических полей, обусловленные генерационно‐рекомбинационными процессами». | |
Аннотация:
|
| Стусь Наталья Сергеевна | |
| Научный руководитель — Румянцев Дмитрий Александрович, доцент кафедры теор. физики, к. ф.‐м. н. | |
| Тема: «Резонансное рождение электрон‐позитронных пар в магнитосфере магнитара». | |
Аннотация:
|
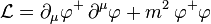 , входящий в теорию двух комплексных скалярных полей, образующих дублет
, входящий в теорию двух комплексных скалярных полей, образующих дублет 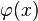 , и инвариантный относительно глобальных преобразований, обладающий U(1)‐глобальной симметрией и фазой
, и инвариантный относительно глобальных преобразований, обладающий U(1)‐глобальной симметрией и фазой 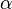 , не зависящей от координат; модифицированный лагранжиан, инвариантный относительно локальных преобразований SU(2), т. е. зависящих от точки пространства‐времени; тензор напряженностей
, не зависящей от координат; модифицированный лагранжиан, инвариантный относительно локальных преобразований SU(2), т. е. зависящих от точки пространства‐времени; тензор напряженностей ![F_{\mu\nu}=\partial_\mu A_\nu-\partial_\nu A_\mu+\frac{g}{\mathrm{i}}\left[A_\mu,A_\nu\right]](/images/math/2/9/d/29d62b5c8ee5eec043a7c6060c8ca8a4.png) ; калибровочно‐инвариантный лагранжиан
; калибровочно‐инвариантный лагранжиан 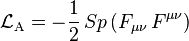 , где
, где 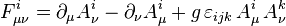 и следующие из него уравнения без материи:
и следующие из него уравнения без материи: 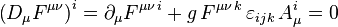 и с материей:
и с материей: 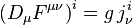 , а также уравнения Янга–Миллса для потенциалов.
, а также уравнения Янга–Миллса для потенциалов.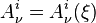 , где
, где 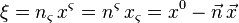 и
и 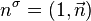 — постоянный 4‐вектор. В частном случае
— постоянный 4‐вектор. В частном случае 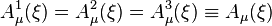 найдено решение уравнений Янга–Миллса, при которых тензор напряженностей поля и уравнения Янга–Миллса переходят в соответствующие классические выражения электродинамики.
найдено решение уравнений Янга–Миллса, при которых тензор напряженностей поля и уравнения Янга–Миллса переходят в соответствующие классические выражения электродинамики.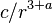 , где
, где 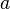 рассматривался как свободный параметр. Хотя размер облака в действительности является конечным, приближение бесконечного облака со степенным законом распределения плотности, с одной стороны, незначительно отличается от истинного распределения на небольших расстояниях от центра, с другой стороны, позволяет провести до конца аналитические вычисления.
рассматривался как свободный параметр. Хотя размер облака в действительности является конечным, приближение бесконечного облака со степенным законом распределения плотности, с одной стороны, незначительно отличается от истинного распределения на небольших расстояниях от центра, с другой стороны, позволяет провести до конца аналитические вычисления.